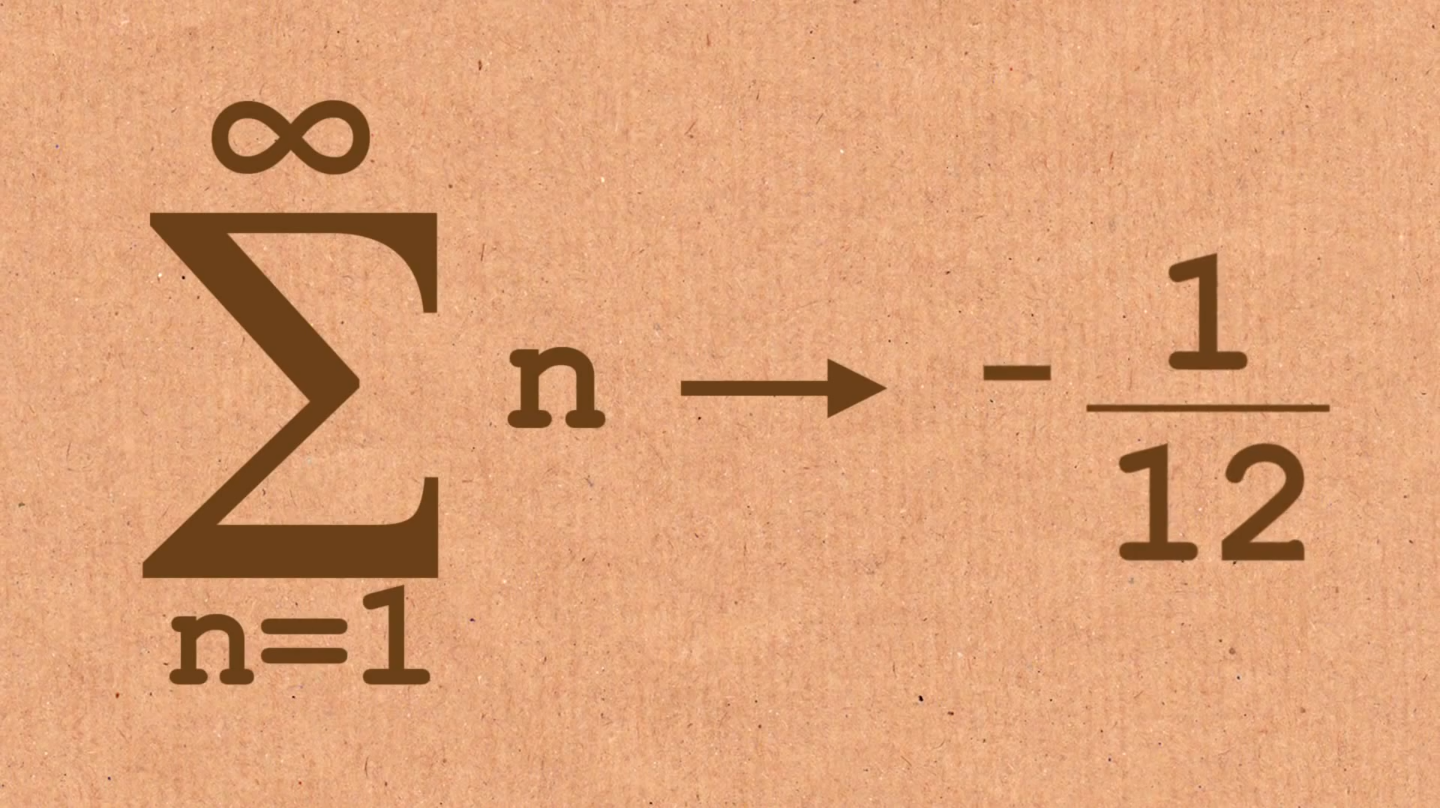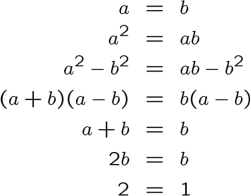The Pinnacle

As my coursework for mathematics at GVSU is coming to a close, I've began to reflect on what I got out of my GVSU mathematical education. I've had experiences that were great and some that were not so great. As a whole, I feel that the coursework was great exposure, but at times was also too much for my future plans.

Some classes that I felt that were most beneficial to my future career as an educator would be MTH 229, MTH 329, and MTH 315. These courses are all either education related or, in my opinion, stretched my thinking to a point where I felt was most beneficial. The education courses helped me immensely as the experience exposure in those courses were the first to truly open up my eyes to the field of mathematical education. I know that before I went into MTH 329, being Mathematical Activities for middle grades, I had no intentions to work in a middle school setting. However, now I feel that I would be open to the opportunity because I have enjoyed the material discussions and working with the students in the middle schools.

For MTH 229, which revolved around mathematical activities for high school, the exposure was nice to see in the high schools as well. However, what was most beneficial to me was seeing two different points of view for teaching through classroom observations. I met one teacher where I would love to see myself being as great as him and another where I would never want to have his style of teaching. The teacher that I really liked had the standard of teaching for I do, we do, you do format, but his interactions with the students was seamless. The teacher had great respect for his students and the students reciprocated the respect right back to him. Also, the students' desks were like whiteboard material, so whenever they were practicing problems, their desks were a form of scrap paper and I loved it. For the teacher that I didn't agree with as much, he basically had the students learn all the material themselves and then had the students come to him if they had any questions. Oddly enough, as I came back to the school, more and more students gravitated towards me and stopped asking the teacher their questions. I felt bad to not keep coming back, as I enjoyed the students' want for my help, but it was a great experience to show me what not to do.

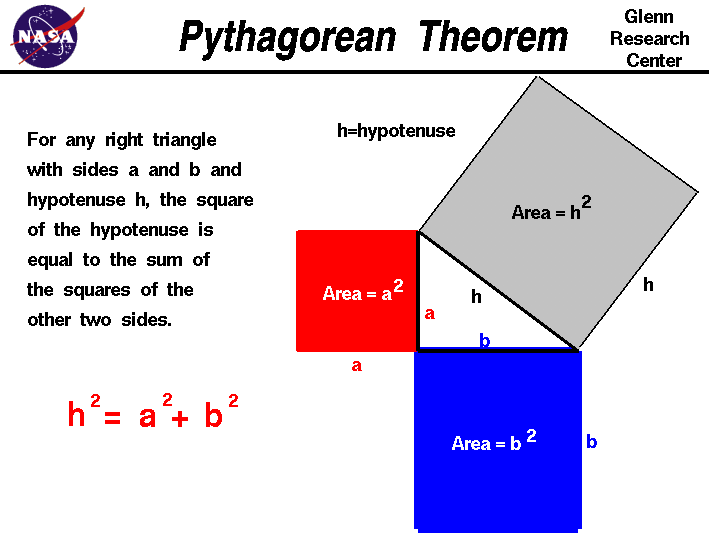
For the last class that I thought contributed the most to my future, MTH 315 Discrete Mathematics, I feel this helped my thinking skills immensely. I felt that the concepts covered in the course are the closest concepts to what I will be teaching in a classroom that wasn't straight from an education mathematics course. Concepts like Graph Theory, Pigeonhole Principle, and many other different ways of counting were very enjoyable. The style of learning was a little odd for me, being student driven and learning in groups, but I adjusted well to it. My style is geared more towards lecture based.

Some courses that I felt were not as constructive were Linear Algebra 2 and Euclidean Geometry. These courses had things that detracted from my learning. For these courses, I felt that my experiences did not work well with the teaching styles so it made the work harder for me than it had to be. One course was very applied when we were tested, but we weren't taught the concepts thoroughly and the other had such a discouraging grading system that I was literally failing the entire semester until exam day. I wasn't failing because I did terrible, it was because of the, in my opinion, broken grading system. Although these courses gave me a tough time, I learned valuable teaching knowledge. I learned to have a fair grading system that works for all students and to not expect more from my students if I haven't taught the material well enough.

After my two and a half years worth of semesters so far, I feel that my mathematical experience has been great. Yes, I have been super frustrated at times and also very happy, but with that I was given a full experience. I will always be proud to be a Laker and be proud of what I was able to accomplish at a four-year university, especially being the first in my family to accomplish such a milestone. I look forward to my future mathematical work and will always know that I can achieve greatness in the field with the solid ground that I have laid by attending GVSU.

Images:

https://www.google.com/url?sa=i&rct=j&q=&esrc=s&source=images&cd=&cad=rja&uact=8&ved=0ahUKEwjy-KG68ezXAhUrzIMKHU3xAxAQjRwIBw&url=https%3A%2F%2Fcencam.org%2Fschool%2Fcambria%2Fteacher%2Fclong%2Fmath%2F&psig=AOvVaw1DeHdY2UQ7D_Rm5QIvugw1&ust=1512357656845726

https://ivyleaguecenter.files.wordpress.com/2015/03/discrete-math.jpg

Was Math Invented or Discovered? BOTH! (Blog Post #4)

One of the most debated questions in all of mathematics is whether or not math was discovered or invented. Do we see mathematics as purely a part of nature? Or is mathematics purely a language that humans have created? Is there a possibility to be both? Can they not be the same? Personally, I believe the answer is both, depending on how you look at mathematics and the way we use and shape it. To understand how mathematics is invented, let's take a look at how mathematics is discovered.

So, how is math discovered? Math is discovered because if we were to eliminate all that humans know about mathematics, mathematics would still be a living, breathing entity that is a part of nature. We can see mathematics in the trees being there's a circumference to its trunk or we can see that the same tree is very tall so it must have a height. How we make sense of these discoveries is why mathematics can be seen as invented because by putting these observations into a language aspect seems to appear as something that someone created, even when the observations have been there all along. It's like saying because a person observed that a tree is tall and they made increments of measurement that they invented mathematics because they simply named a tree's height a measurement. This isn't true that the height was created, as it was there before an individual walked up to it, it's to say that someone claimed the tree to have a relation to the label that the individual decided to slap on it. Mathematics is incorporated into every aspect of life, it's up to humans to discover those aspects and invent a language to convey those findings to others.

So, then how is math invented? Simply put, mathematics is invented by the way we describe it formally. When someone first discovered the usage of mathematics, they weren't sure what to call it except for something they decided was a good label to mark it as. From there, mathematics was experimented with and new aspects soon were discovered and put into an invented language form so that others could understand the complexities that go along with mathematics. By discovering aspects that were deemed true by means of proof, humans were able to invent a set of rules that work for all means of possibilities with a given property. Going back to the tree example, it is clear that a tree would have its height no matter what, but as said before, humans only placed a relation label on the tree's height to make sense of its relation to other things we can relate the tree to. For example, the use of an invented form of measurement can be used to make sense of how big the tree is compared to a human being or another tree perhaps. The language of mathematics was invented, not the nature of mathematics.

Some people may say that mathematics cannot be both discovered and invented. How can something be discovered if we simply made it up and called it an invention? Inventions, on the contrary, are discoveries in themselves. However, inventions are not discoveries. This can be tricky because the relationship does not go both ways. To invent something means that one made a discovery to create a new object or idea. However, one does not invent a discovery, unless someone is making something up that is false or hasn't been proven. A discovery itself, by definition, is "the action or process of discovering," and discovering is "find (something or someone) unexpectedly or in the course of a search." When one invents something, they aren't simply gazing upon the object or idea and simply it is there. No mathematician walked up to an object when mathematics was first discovered and thought "so this is math." No, they had to see the discovery and then invent a language to convey this discovery. An invention requires building or creating something which is why the language of mathematics is invented and the nature of mathematics is discovered. (Google)

 

 Mathematics is the logic of nature. By discovering the properties that mathematics possesses, people are able to invent a language to convey one's findings, or discoveries, about different aspects of mathematics. By discovering aspects of mathematics and inventing a language of mathematics, we can communicate properly and share ideas of what mysteries mathematics still has in store. What do you think? Was math discovered? Was math invented? Is it both?

Sources:

https://www.google.com/search?q=definition+of+discovery&ie=utf-8&oe=utf-8

https://www.google.com/search?ei=LCILWuuhF4zIjwTq7ovABA&q=definition+of+discovering&oq=definition+of+discovering&gs_l=psy-ab.3..0j0i22i30k1l2.50260.50978.0.51279.4.4.0.0.0.0.176.559.0j4.4.0....0...1.1.64.psy-ab..0.4.555...0i67k1.0.j0ihrPeNmeE

Images:

https://wonderopolis.org/_img?img=/wp-content/uploads/2014/06/dreamstime_xl_19206361-Custom.jpg&transform=resizeCrop,720,450

https://openclipart.org/image/2400px/svg_to_png/263892/Colorful-Natural-Tree.png

https://az616578.vo.msecnd.net/files/2016/09/07/636088716923509308-1951112735_Debate-debate-22744126-1167-854.jpg

Gullible Mathematics

Have you ever thought about how gullible people can be when encountering mathematics? Mathematics is so powerful that it can easily be taken for granted. I find myself being a victim of this unfortunate situation from time to time when I am a student and when I tutor, both myself and tutees being gullible at times in tutoring situations. How does this happen? How can this be prevented? Let's take a look.

I recently watched a Numberphile video about how the sum of all positive integers is -1/12, I thought that is a mistake. However, the more I watched the video, I found myself becoming a believer, oddly. Internally, I feel there is no way to sum up positive integers and result in a negative answer. In this case, I didn't want to take my own word for it, so I took it upon myself to ask my fellow co-workers at Grand Rapids Community College that I work with in the Mathematics Tutorial Lab.

The reactions in the Math Lab were surprising to me. This notion that all positive numbers could possibly equate to a negative number was borderline enraging. One of my co-workers was almost yelling at me, not entirely knowing he was at the time, about saying how ridiculous it is to think that the result could be a negative number. He was so passionate about how much it upsets him that people could argue that the sum of all positive integers could become a negative number. We talked a little bit about how the explanation worked and how there was one part of the proof where the presenter basically said "this happens because it does" and it bothered us because we couldn't see where that explanation comes from. This made us think that people in general could be tricked into thinking almost anything mathematical if this is a possibility to convince people of something that isn't true by being said with such confidence. Now let's discuss how misconceptions can be brought up from my personal experiences working with mathematics.

On some rare occasions, when I work with tutees, one of us gets so convinced by the other's error that we accept it to be true for quite some time until we stare at the issue occurring for a while. For example, a student could have a reasonable explanation for a problem except for one small issue, typically a sign on most occasions, and I'll read it and deem it to be viable and confused how they got the wrong answer. This also can happen when I am explaining a problem to someone where I may miss a sign and get to the end only to be told I am wrong from the back of the book. The point here is, though, if someone sounds confident about their mathematics, they are so much more convincing that they are correct. Mistakes can be more accepted when said with confidence... I also know that this isn't just an occasion where I am the issue because I have discussed this issue with other co-workers that have felt the same about certain instances just like those stated.

So what's the point? Why does it matter if people are gullible to mathematics? The point is that in order for us to avoid how gullible people can be to the topic is to inform people why the unique aspects of mathematics truly works. As a future educator, I know the most important contribution I can make to my students would be to inform them on why concepts can and cannot work when they are trying to problem solve. A prime example that would be a goal of mine would be to have every single one of my students be able to look at the proof as to why someone conjectured that 2 = 1 and be able to tell me why that proof doesn't work.

So how does this spawn into a student's mind? How can a student internalize a concept without questioning it? The answer is how K - 12 education can cater to standardized testing and not always support their students by addressing the real reason why students are learning the Common Core State Standards. Many students, if questioned why something works, would say "it just does" or "it's what my teacher said." This isn't acceptable as this leads to misconceptions and not being able to look at a proof, like the one that concludes that the sum of all positive integers is a negative number, and say that something isn't quite right here. One of the easiest solutions to helping with misconceptions would be to teach the correct concepts initially and then let students question the concepts instead of internalizing that things are the way they are "just because."

Educators of the future must keep in mind the precious ability to mold minds. By stressing the concepts instead of "going through the motions," we can better the outcome of students grasping mathematics instead of sliding through the cracks.

Images:

http://skullsinthestars.files.wordpress.com/2008/12/2equals1.png?w=252&h=196

https://previews.123rf.com/images/wavebreakmediamicro/wavebreakmediamicro1406/wavebreakmediamicro140603707/29007855-Angry-businesswoman-gesturing-against-math-in-thought-bubble-Stock-Photo.jpg

https://i.warosu.org/data/sci/img/0066/21/1404236448233.png

Book Review: Quite Right - The Story of Mathematics, Measurement, and Money

            Have you ever wondered how mathematics was used with little to no verbal language? Have you ever wondered why we calculate time the way we do in base 60? Or have you simply even wondered how currency came about? If you answered yes to any of these questions with a spark of interest, then Quite Right: The Story of Mathematics, Measurement, and Money, by Norman Biggs, is the book for you! Through the progression of this book, you will learn many aspects of the history of mathematics, measurement, and money.

            Some strong points of this book are the explanations and the amount of content covered. Throughout the book, the reader will be taken through many different mathematical concepts that have been around for centuries and how those concepts played a role in society based on the given region’s culture. Readers will be able to visit places like Egypt and visit people like the Babylonians! This book does use the history of mathematics as a stronghold for the content area, but it also has a lot of solid tie-in material that involve forms of measurement and money. 

            Some of the weak points of the book have to deal with the disbursement of content and the ability to comprehend certain mathematical topics. As said before, the history of mathematics is the majority of this book, so if one is going in hoping to learn more about measurement or money, it would be best to find a different book. However, if a solid mix in of measurement and money is well enough, then this is an excellent choice! Along with some disbursement issues, the pacing can be odd as well, but can be overlooked quickly with the next upcoming possibly more interesting topic. The recommended mathematical reading level definitely requires some college level mathematics, as the mathematics can go fairly in depth and abstract enough where some deeper mathematical knowledge is required.

            All in all, anyone that is looking for some interesting facts about the history of mathematics, measurement, and money, then this is a great read! As long as the reader has a fairly good sense of mathematics, the book will be a pleasant experience to read through. I would say that this book gave me a greater understanding of why mathematics is a thing in society from a theoretical point of view. For a rating, I would give this book a solid 7.5 out of 10.

Images:

https://www.google.com/imgres?imgurl=https%3A%2F%2Fimages-na.ssl-images-amazon.com%2Fimages%2FI%2F41fWgXwXWcL._SX325_BO1%2C204%2C203%2C200_.jpg&imgrefurl=https%3A%2F%2Fwww.amazon.com%2FQuite-Right-Story-Mathematics-Measurement-ebook%2Fdp%2FB019GXM8VA&docid=ICjwX_GNKE4ItM&tbnid=s2-t7q3M7dpflM%3A&vet=10ahUKEwj6-8mp_t7WAhUDRyYKHZP6AlgQMwgmKAAwAA..i&w=327&h=499&bih=807&biw=1368&q=quite%20right%20the%20story%20of%20mathematics%20measurement%20and%20money&ved=0ahUKEwj6-8mp_t7WAhUDRyYKHZP6AlgQMwgmKAAwAA&iact=mrc&uact=8

Pythagoras: The Man, the Math, the Religion (Blogpost1)

Pythagoras has been known as one of the purest mathematicians of all time. Some feel he was so pure that he should be treated as a divine individual. Although he is known for being a mathematician, in many ways people argue he was never the creator of his accredited work. For example, when he made his famous trip to Egypt, he came back and said he had discovered what is known as the Pythagorean Theorem. However, it has been argued many times that Pythagoras simply took the idea from Egypt and told his friends back home basically it was something he came up with. This notion of stealing credit comes up a lot in Pythagoras' life, another instance being when he created his own secret society of mathematicians that came up with a lot of well known ideas still used in today's world.

Pythagoras was a man that seemed to be full of himself. This can be interpreted as Pythagoras created his own secret society and his followers treated him as a God. In order to be admitted to the secret society, one must have the sacred symbol on one's hand known as the pentad, or five pointed star. While in the secret society, many of the followers tried to collaborate with Pythagoras in order to discover new ways of using mathematics. One of the downfalls of being a follower and coming up with a new great idea was that most of the time Pythagoras received the credit for said new idea. It is believed that even Pythagoras himself didn't contribute to much of what his name holds to today as he simply took his followers' work and slapped his name on it or potentially killed you. In fact, it is said that when one of his followers thought of irrational numbers, Pythagoras simply drowned the individual and made the rest of his followers swear to never speak of his action again. Pythagoras and his secret society shared many ideas that have been well developed to stand the test of time.


In many ways, the mathematics presented by Pythagoras is used in present time. Of course, there's usage like the Pythagorean Theorem is schools and such, but there's also uses such as in art pieces or architecture. One of these instances is known as the golden rectangle. The golden rectangle is a rectangle that infinitesimally halves itself by continuously drawing rectangles within a rectangle that are half the size of the previous one. The process of of doing this creates a spiral motion. Along with the spiral, the golden rectangle was used in a lot of Western architecture and art such as paintings of people and buildings. The idea of the golden rectangle was so popular that it is still used in modern day architecture when designing new buildings. In one other form of art, being music, Pythagoras also made a significant contribution by discovering octaves. Pythagoras and his group of followers discovered that when a musical string is plucked, the next highest octave can be found by shortening the string by half and then plucking the string. Obviously, this is still used in today's world as music is still a prominent form of culture.

                                                               (the golden rectangle)


Pythagoras certainly lived an interesting life, but it is hardly known how exactly he died. It is known, however, that he died in 495 BC. Unfortunately, not enough evidence supports one possibility strong enough to deduce how he passed.

Why should students learn about Pythagoras? Simply to understand the truth of his life. Most students find mathematics boring and non-enjoyable. By learning about Pythagoras, with how interesting his history is, students may give more attention to the curriculum. If students learned how Pythagoras influenced music or how he was said to be a leader of a cult, anything is possible to grasp student attention. A small instruction about Pythagoras while learning the Pythagorean Theorem may be a way to engage students more and enrich their knowledge outside of the standard curriculum.

So, what has Pythagoras brought to the mathematical world? Some say he made significant contributions to the mathematical world and some would say that he presented a lot to the mathematical world. With the speculation that Pythagoras simply took many individuals' ideas and made them as his own merit, it's hard to decipher whether he made mathematical contributions to the world. It is safe to safe that he presented to the world a lot of helpful ideas in mathematics, but to some that's about all we can say for him. There's no question that Pythagoras was smart as he was a  major player in being a mathematician and having his own religion, but nobody will ever really know how much he contributed of his own ideas to the world. Pythagoras is the man, the math, and the religion of his time, but his own ideas may be something of simply a myth or a legend.

Image Links:

https://www.google.com/url?sa=i&rct=j&q=&esrc=s&source=images&cd=&cad=rja&uact=8&ved=0ahUKEwiFzYrh66zWAhWK0YMKHQjoBTMQjRwIBw&url=https%3A%2F%2Fwww.thefamouspeople.com%2Fprofiles%2Fpythagoras-504.php&psig=AFQjCNFxk7y2LWcrhuHBvsHje8txoyXrJg&ust=1505759060400087

https://www.grc.nasa.gov/www/k-12/airplane/Images/pythag.gif

https://farm1.staticflickr.com/16/21152695_35a8e05d1a_o.png

What is Math?

What is Math?

          Math is the merging of numeric values and letters with concepts and patterns. We use mathematics as a tool to prove many different concepts based on different types of noticeable patterns in different situations by using numeric values and letter values that correspond to unknown values. Once someone sees a pattern, they try to find a way to internalize that pattern and either make sense of it or try to use it to predict a future outcome. This can be seen as the use of logic, as mathematics can be a branch of logic.

           Math is also one element in life that is always defined when rules are followed. When used with proper application rules, math can never be wrong as it is a fixed entity that cannot be broken. If one is correct with their arithmetic in mathematics, one can never be proven wrong as math is a concrete system. It's not a subjective topic such as an English application where many different answers can be said about a given situation whereas mathematics has a clear cut answer. There may be many different roads to a given answer, but there is always one correct endpoint in solving mathematics.

          The top 5 biggest moments in mathematics are the identification of an imaginary number, the ability to conceptualize patterns, the ability to form formulas to predict future occurrences, the defining of pi, and the conceptualization of graph theory. I feel these are the top 5 biggest moments in mathematics because the imaginary number has many applications to it, the ability to conceptualize patterns allows us to use such patterns to either predict future occurrences or see trends within a pattern, defining pi has allowed us to expand our knowledge on circular shapes, and using graphs to have a visualization of the different formulas and patterns that we create from many different situations. These five big moments are huge because they define a lot of topics that are used to teach the young minds of the nation and they must be important if they are part of the chosen few to have students exposed to in their K-12 experiences.