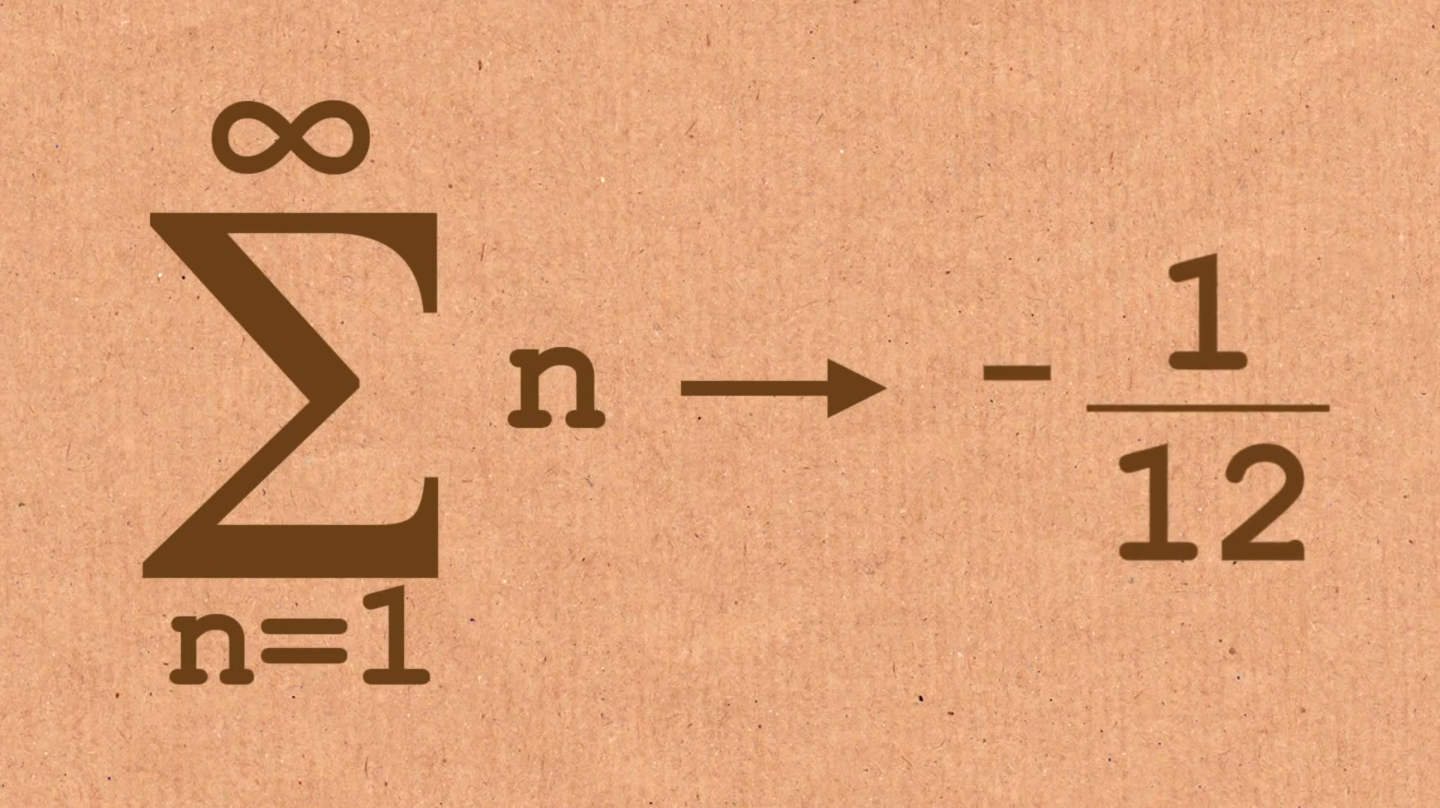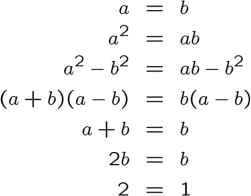Some classes that I felt that were most beneficial to my future career as an educator would be MTH 229, MTH 329, and MTH 315. These courses are all either education related or, in my opinion, stretched my thinking to a point where I felt was most beneficial. The education courses helped me immensely as the experience exposure in those courses were the first to truly open up my eyes to the field of mathematical education. I know that before I went into MTH 329, being Mathematical Activities for middle grades, I had no intentions to work in a middle school setting. However, now I feel that I would be open to the opportunity because I have enjoyed the material discussions and working with the students in the middle schools.
Some classes that I felt that were most beneficial to my future career as an educator would be MTH 229, MTH 329, and MTH 315. These courses are all either education related or, in my opinion, stretched my thinking to a point where I felt was most beneficial. The education courses helped me immensely as the experience exposure in those courses were the first to truly open up my eyes to the field of mathematical education. I know that before I went into MTH 329, being Mathematical Activities for middle grades, I had no intentions to work in a middle school setting. However, now I feel that I would be open to the opportunity because I have enjoyed the material discussions and working with the students in the middle schools.For MTH 229, which revolved around mathematical activities for high school, the exposure was nice to see in the high schools as well. However, what was most beneficial to me was seeing two different points of view for teaching through classroom observations. I met one teacher where I would love to see myself being as great as him and another where I would never want to have his style of teaching. The teacher that I really liked had the standard of teaching for I do, we do, you do format, but his interactions with the students was seamless. The teacher had great respect for his students and the students reciprocated the respect right back to him. Also, the students' desks were like whiteboard material, so whenever they were practicing problems, their desks were a form of scrap paper and I loved it. For the teacher that I didn't agree with as much, he basically had the students learn all the material themselves and then had the students come to him if they had any questions. Oddly enough, as I came back to the school, more and more students gravitated towards me and stopped asking the teacher their questions. I felt bad to not keep coming back, as I enjoyed the students' want for my help, but it was a great experience to show me what not to do.
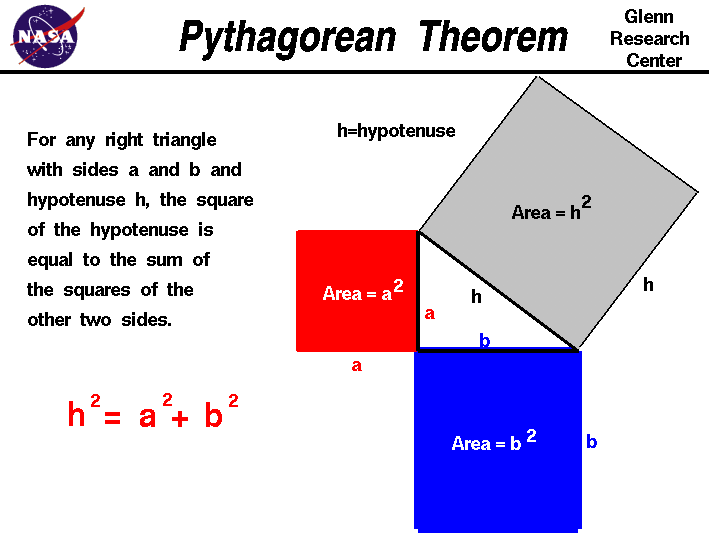
 For the last class that I thought contributed the most to my future, MTH 315 Discrete Mathematics, I feel this helped my thinking skills immensely. I felt that the concepts covered in the course are the closest concepts to what I will be teaching in a classroom that wasn't straight from an education mathematics course. Concepts like Graph Theory, Pigeonhole Principle, and many other different ways of counting were very enjoyable. The style of learning was a little odd for me, being student driven and learning in groups, but I adjusted well to it. My style is geared more towards lecture based.
For the last class that I thought contributed the most to my future, MTH 315 Discrete Mathematics, I feel this helped my thinking skills immensely. I felt that the concepts covered in the course are the closest concepts to what I will be teaching in a classroom that wasn't straight from an education mathematics course. Concepts like Graph Theory, Pigeonhole Principle, and many other different ways of counting were very enjoyable. The style of learning was a little odd for me, being student driven and learning in groups, but I adjusted well to it. My style is geared more towards lecture based.Some courses that I felt were not as constructive were Linear Algebra 2 and Euclidean Geometry. These courses had things that detracted from my learning. For these courses, I felt that my experiences did not work well with the teaching styles so it made the work harder for me than it had to be. One course was very applied when we were tested, but we weren't taught the concepts thoroughly and the other had such a discouraging grading system that I was literally failing the entire semester until exam day. I wasn't failing because I did terrible, it was because of the, in my opinion, broken grading system. Although these courses gave me a tough time, I learned valuable teaching knowledge. I learned to have a fair grading system that works for all students and to not expect more from my students if I haven't taught the material well enough.
After my two and a half years worth of semesters so far, I feel that my mathematical experience has been great. Yes, I have been super frustrated at times and also very happy, but with that I was given a full experience. I will always be proud to be a Laker and be proud of what I was able to accomplish at a four-year university, especially being the first in my family to accomplish such a milestone. I look forward to my future mathematical work and will always know that I can achieve greatness in the field with the solid ground that I have laid by attending GVSU.
Images:
https://www.google.com/url?sa=i&rct=j&q=&esrc=s&source=images&cd=&cad=rja&uact=8&ved=0ahUKEwjy-KG68ezXAhUrzIMKHU3xAxAQjRwIBw&url=https%3A%2F%2Fcencam.org%2Fschool%2Fcambria%2Fteacher%2Fclong%2Fmath%2F&psig=AOvVaw1DeHdY2UQ7D_Rm5QIvugw1&ust=1512357656845726
https://ivyleaguecenter.files.wordpress.com/2015/03/discrete-math.jpg