Gullible Mathematics

Have you ever thought about how gullible people can be when encountering mathematics? Mathematics is so powerful that it can easily be taken for granted. I find myself being a victim of this unfortunate situation from time to time when I am a student and when I tutor, both myself and tutees being gullible at times in tutoring situations. How does this happen? How can this be prevented? Let's take a look.

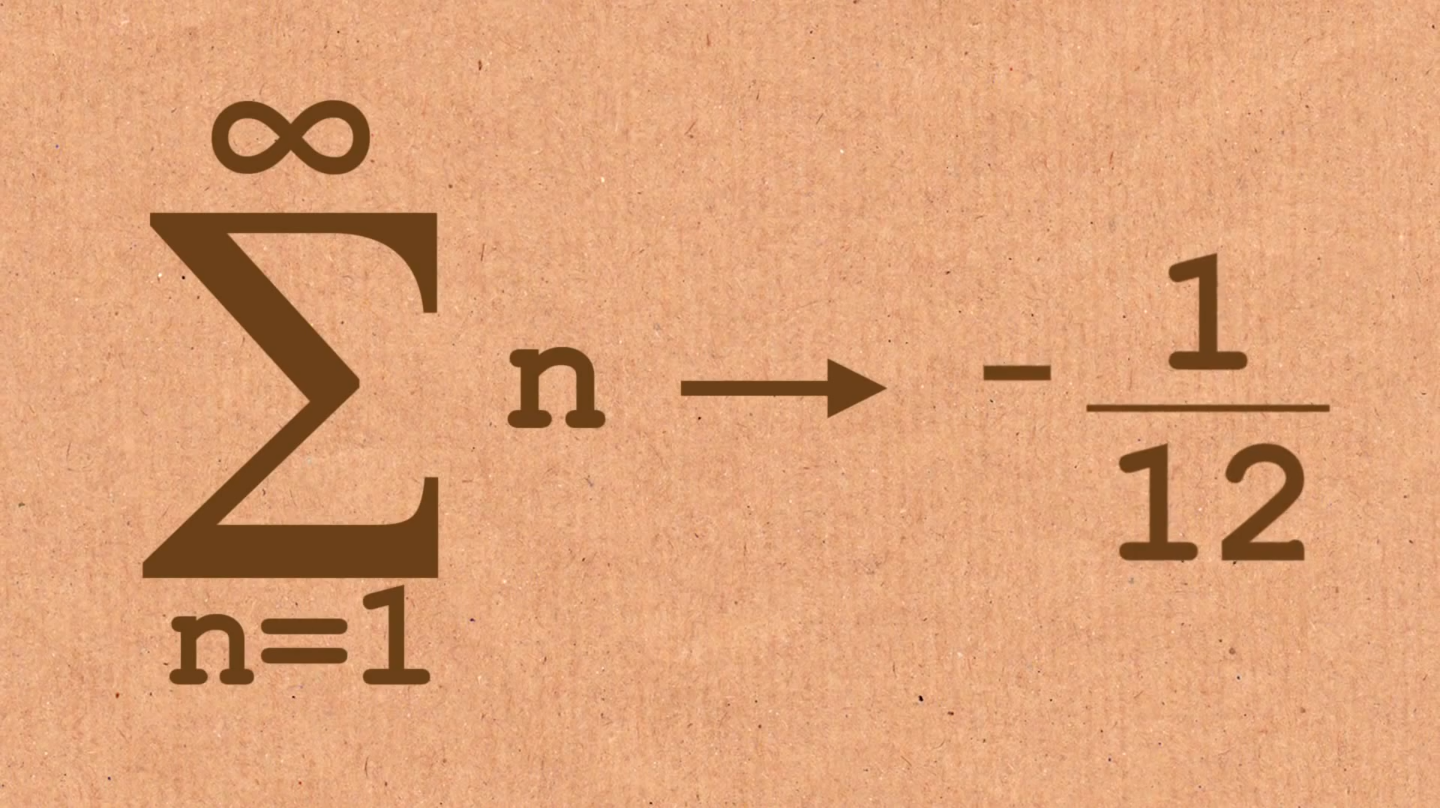I recently watched a Numberphile video about how the sum of all positive integers is -1/12, I thought that is a mistake. However, the more I watched the video, I found myself becoming a believer, oddly. Internally, I feel there is no way to sum up positive integers and result in a negative answer. In this case, I didn't want to take my own word for it, so I took it upon myself to ask my fellow co-workers at Grand Rapids Community College that I work with in the Mathematics Tutorial Lab.

The reactions in the Math Lab were surprising to me. This notion that all positive numbers could possibly equate to a negative number was borderline enraging. One of my co-workers was almost yelling at me, not entirely knowing he was at the time, about saying how ridiculous it is to think that the result could be a negative number. He was so passionate about how much it upsets him that people could argue that the sum of all positive integers could become a negative number. We talked a little bit about how the explanation worked and how there was one part of the proof where the presenter basically said "this happens because it does" and it bothered us because we couldn't see where that explanation comes from. This made us think that people in general could be tricked into thinking almost anything mathematical if this is a possibility to convince people of something that isn't true by being said with such confidence. Now let's discuss how misconceptions can be brought up from my personal experiences working with mathematics.

On some rare occasions, when I work with tutees, one of us gets so convinced by the other's error that we accept it to be true for quite some time until we stare at the issue occurring for a while. For example, a student could have a reasonable explanation for a problem except for one small issue, typically a sign on most occasions, and I'll read it and deem it to be viable and confused how they got the wrong answer. This also can happen when I am explaining a problem to someone where I may miss a sign and get to the end only to be told I am wrong from the back of the book. The point here is, though, if someone sounds confident about their mathematics, they are so much more convincing that they are correct. Mistakes can be more accepted when said with confidence... I also know that this isn't just an occasion where I am the issue because I have discussed this issue with other co-workers that have felt the same about certain instances just like those stated.

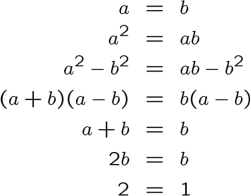So what's the point? Why does it matter if people are gullible to mathematics? The point is that in order for us to avoid how gullible people can be to the topic is to inform people why the unique aspects of mathematics truly works. As a future educator, I know the most important contribution I can make to my students would be to inform them on why concepts can and cannot work when they are trying to problem solve. A prime example that would be a goal of mine would be to have every single one of my students be able to look at the proof as to why someone conjectured that 2 = 1 and be able to tell me why that proof doesn't work.

So how does this spawn into a student's mind? How can a student internalize a concept without questioning it? The answer is how K - 12 education can cater to standardized testing and not always support their students by addressing the real reason why students are learning the Common Core State Standards. Many students, if questioned why something works, would say "it just does" or "it's what my teacher said." This isn't acceptable as this leads to misconceptions and not being able to look at a proof, like the one that concludes that the sum of all positive integers is a negative number, and say that something isn't quite right here. One of the easiest solutions to helping with misconceptions would be to teach the correct concepts initially and then let students question the concepts instead of internalizing that things are the way they are "just because."

Educators of the future must keep in mind the precious ability to mold minds. By stressing the concepts instead of "going through the motions," we can better the outcome of students grasping mathematics instead of sliding through the cracks.

Images:

http://skullsinthestars.files.wordpress.com/2008/12/2equals1.png?w=252&h=196

https://previews.123rf.com/images/wavebreakmediamicro/wavebreakmediamicro1406/wavebreakmediamicro140603707/29007855-Angry-businesswoman-gesturing-against-math-in-thought-bubble-Stock-Photo.jpg

https://i.warosu.org/data/sci/img/0066/21/1404236448233.png