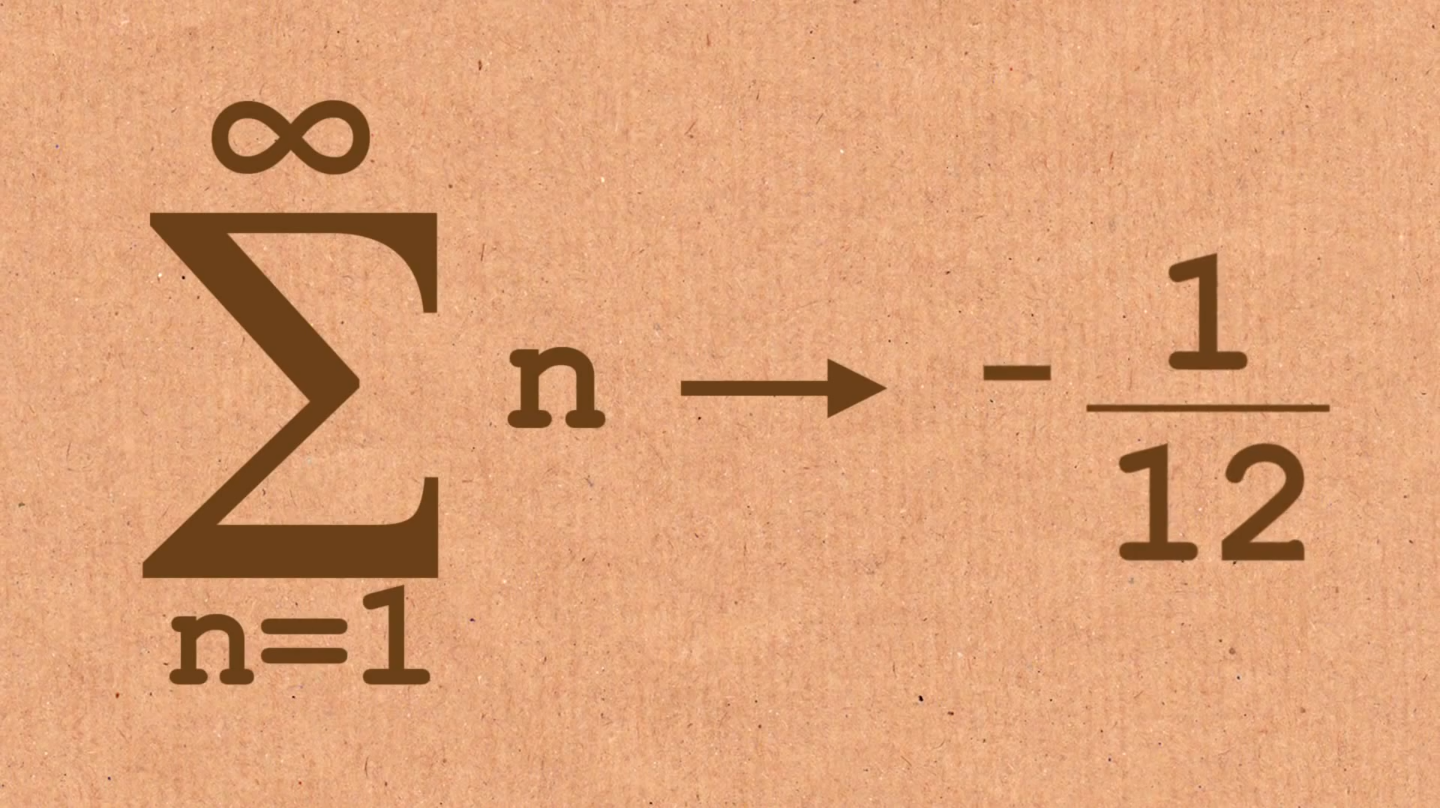Was Math Invented or Discovered? BOTH! (Blog Post #4)

One of the most debated questions in all of mathematics is whether or not math was discovered or invented. Do we see mathematics as purely a part of nature? Or is mathematics purely a language that humans have created? Is there a possibility to be both? Can they not be the same? Personally, I believe the answer is both, depending on how you look at mathematics and the way we use and shape it. To understand how mathematics is invented, let's take a look at how mathematics is discovered.

So, how is math discovered? Math is discovered because if we were to eliminate all that humans know about mathematics, mathematics would still be a living, breathing entity that is a part of nature. We can see mathematics in the trees being there's a circumference to its trunk or we can see that the same tree is very tall so it must have a height. How we make sense of these discoveries is why mathematics can be seen as invented because by putting these observations into a language aspect seems to appear as something that someone created, even when the observations have been there all along. It's like saying because a person observed that a tree is tall and they made increments of measurement that they invented mathematics because they simply named a tree's height a measurement. This isn't true that the height was created, as it was there before an individual walked up to it, it's to say that someone claimed the tree to have a relation to the label that the individual decided to slap on it. Mathematics is incorporated into every aspect of life, it's up to humans to discover those aspects and invent a language to convey those findings to others.

So, then how is math invented? Simply put, mathematics is invented by the way we describe it formally. When someone first discovered the usage of mathematics, they weren't sure what to call it except for something they decided was a good label to mark it as. From there, mathematics was experimented with and new aspects soon were discovered and put into an invented language form so that others could understand the complexities that go along with mathematics. By discovering aspects that were deemed true by means of proof, humans were able to invent a set of rules that work for all means of possibilities with a given property. Going back to the tree example, it is clear that a tree would have its height no matter what, but as said before, humans only placed a relation label on the tree's height to make sense of its relation to other things we can relate the tree to. For example, the use of an invented form of measurement can be used to make sense of how big the tree is compared to a human being or another tree perhaps. The language of mathematics was invented, not the nature of mathematics.

Some people may say that mathematics cannot be both discovered and invented. How can something be discovered if we simply made it up and called it an invention? Inventions, on the contrary, are discoveries in themselves. However, inventions are not discoveries. This can be tricky because the relationship does not go both ways. To invent something means that one made a discovery to create a new object or idea. However, one does not invent a discovery, unless someone is making something up that is false or hasn't been proven. A discovery itself, by definition, is "the action or process of discovering," and discovering is "find (something or someone) unexpectedly or in the course of a search." When one invents something, they aren't simply gazing upon the object or idea and simply it is there. No mathematician walked up to an object when mathematics was first discovered and thought "so this is math." No, they had to see the discovery and then invent a language to convey this discovery. An invention requires building or creating something which is why the language of mathematics is invented and the nature of mathematics is discovered. (Google)

 

 Mathematics is the logic of nature. By discovering the properties that mathematics possesses, people are able to invent a language to convey one's findings, or discoveries, about different aspects of mathematics. By discovering aspects of mathematics and inventing a language of mathematics, we can communicate properly and share ideas of what mysteries mathematics still has in store. What do you think? Was math discovered? Was math invented? Is it both?

Sources:

https://www.google.com/search?q=definition+of+discovery&ie=utf-8&oe=utf-8

https://www.google.com/search?ei=LCILWuuhF4zIjwTq7ovABA&q=definition+of+discovering&oq=definition+of+discovering&gs_l=psy-ab.3..0j0i22i30k1l2.50260.50978.0.51279.4.4.0.0.0.0.176.559.0j4.4.0....0...1.1.64.psy-ab..0.4.555...0i67k1.0.j0ihrPeNmeE

Images:

https://wonderopolis.org/_img?img=/wp-content/uploads/2014/06/dreamstime_xl_19206361-Custom.jpg&transform=resizeCrop,720,450

https://openclipart.org/image/2400px/svg_to_png/263892/Colorful-Natural-Tree.png

https://az616578.vo.msecnd.net/files/2016/09/07/636088716923509308-1951112735_Debate-debate-22744126-1167-854.jpg

Gullible Mathematics

Have you ever thought about how gullible people can be when encountering mathematics? Mathematics is so powerful that it can easily be taken for granted. I find myself being a victim of this unfortunate situation from time to time when I am a student and when I tutor, both myself and tutees being gullible at times in tutoring situations. How does this happen? How can this be prevented? Let's take a look.

I recently watched a Numberphile video about how the sum of all positive integers is -1/12, I thought that is a mistake. However, the more I watched the video, I found myself becoming a believer, oddly. Internally, I feel there is no way to sum up positive integers and result in a negative answer. In this case, I didn't want to take my own word for it, so I took it upon myself to ask my fellow co-workers at Grand Rapids Community College that I work with in the Mathematics Tutorial Lab.

The reactions in the Math Lab were surprising to me. This notion that all positive numbers could possibly equate to a negative number was borderline enraging. One of my co-workers was almost yelling at me, not entirely knowing he was at the time, about saying how ridiculous it is to think that the result could be a negative number. He was so passionate about how much it upsets him that people could argue that the sum of all positive integers could become a negative number. We talked a little bit about how the explanation worked and how there was one part of the proof where the presenter basically said "this happens because it does" and it bothered us because we couldn't see where that explanation comes from. This made us think that people in general could be tricked into thinking almost anything mathematical if this is a possibility to convince people of something that isn't true by being said with such confidence. Now let's discuss how misconceptions can be brought up from my personal experiences working with mathematics.

On some rare occasions, when I work with tutees, one of us gets so convinced by the other's error that we accept it to be true for quite some time until we stare at the issue occurring for a while. For example, a student could have a reasonable explanation for a problem except for one small issue, typically a sign on most occasions, and I'll read it and deem it to be viable and confused how they got the wrong answer. This also can happen when I am explaining a problem to someone where I may miss a sign and get to the end only to be told I am wrong from the back of the book. The point here is, though, if someone sounds confident about their mathematics, they are so much more convincing that they are correct. Mistakes can be more accepted when said with confidence... I also know that this isn't just an occasion where I am the issue because I have discussed this issue with other co-workers that have felt the same about certain instances just like those stated.

So what's the point? Why does it matter if people are gullible to mathematics? The point is that in order for us to avoid how gullible people can be to the topic is to inform people why the unique aspects of mathematics truly works. As a future educator, I know the most important contribution I can make to my students would be to inform them on why concepts can and cannot work when they are trying to problem solve. A prime example that would be a goal of mine would be to have every single one of my students be able to look at the proof as to why someone conjectured that 2 = 1 and be able to tell me why that proof doesn't work.

So how does this spawn into a student's mind? How can a student internalize a concept without questioning it? The answer is how K - 12 education can cater to standardized testing and not always support their students by addressing the real reason why students are learning the Common Core State Standards. Many students, if questioned why something works, would say "it just does" or "it's what my teacher said." This isn't acceptable as this leads to misconceptions and not being able to look at a proof, like the one that concludes that the sum of all positive integers is a negative number, and say that something isn't quite right here. One of the easiest solutions to helping with misconceptions would be to teach the correct concepts initially and then let students question the concepts instead of internalizing that things are the way they are "just because."

Educators of the future must keep in mind the precious ability to mold minds. By stressing the concepts instead of "going through the motions," we can better the outcome of students grasping mathematics instead of sliding through the cracks.

Images:

http://skullsinthestars.files.wordpress.com/2008/12/2equals1.png?w=252&h=196

https://previews.123rf.com/images/wavebreakmediamicro/wavebreakmediamicro1406/wavebreakmediamicro140603707/29007855-Angry-businesswoman-gesturing-against-math-in-thought-bubble-Stock-Photo.jpg

https://i.warosu.org/data/sci/img/0066/21/1404236448233.png